Регулярные множества, языки и выражения.

Определение регулярного множества

Определим над множествами цепочек символов из алфавита V операции конка­тенации и итерации следующим образом:

PQ - конкатенация 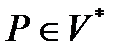и : ;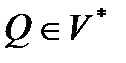

P* - итерация : .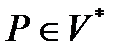

Тогда для алфавита V регулярные множества определяются рекурсивно:

1. 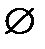— регулярное множество;

2. {λ} — регулярное множество;

3. {а} — регулярное множество ;

4. если Р и Q — произвольные регулярные множества, то множества также являются регулярными множествами;

5. ничто другое не является регулярным множеством.

Фактически регулярные множества — это множества цепочек символов над за­данным алфавитом, построенные определенным образом (с использованием опе­раций объединения, конкатенации и итерации). Все регулярные языки представляют собой регулярные множества.

Регулярные выражения. Свойства регулярных выражений

Регулярные множества можно обозначать с помощью регулярных выражений. Эти обозначения вводятся следующим образом:

1. 0 — регулярное выражение, обозначающее ;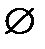

2. λ — регулярное выражение, обозначающее {λ};

3. а — регулярное выражение, обозначающее {a} ;

4. если р и q - регулярные выражения, обозначающие регулярные множества Р и Q, то р + q, pq, p* - регулярные выражения, обозначающие регулярные мно­жества соответственно.

Два регулярных выражения αиβ равны α= β, если они обозначают одно и то же множество.

Каждое регулярное выражение обозначает одно и только одно регулярное мно­жество, но для одного регулярного множества может существовать сколь угодно много регулярных выражений, обозначающих это множество.

При записи регулярных выражений будут использоваться круглые скобки, как и для обычных арифметических выражений. При отсутствии скобок операции выполняются слева направо с учетом приоритета. Приоритет для операций при­нят следующий: первой выполняется итерация (высший приоритет), затем кон­катенация, потом — объединение множеств (низший приоритет).

Если α, β и γ — регулярные выражения, то свойства регулярных выражений можно записать в виде следующих формул:

1.

2.

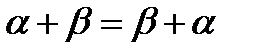
3.

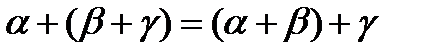
4.

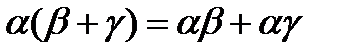
5.

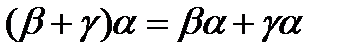
6.

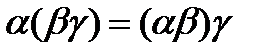
7.

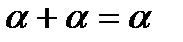
8.

9.

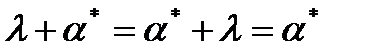
10.

11.

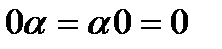
12.

13.

14. .

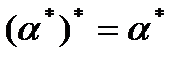Все эти свойства можно легко доказать, основываясь на теории множеств, так как регулярные выражения — это только обозначения для соответствующих множеств.

Следует также обратить внимание на то, что среди прочих свойств отсутствует равенство , то есть операция конкатенации не обладает свойством ком­мутативности. Это и не удивительно, поскольку для этой операции важен поря­док следования символов.

Свойства регулярных языков

Множество называется замкнутым относительно некоторой операции, если в резуль­тате выполнения этой операции над любыми элементами, принадлежащими дан­ному множеству, получается новый элемент, принадлежащий тому же множеству.. Например, множество целых чисел замкнуто относительно операций сложения, умножения и вычитания, но оно не замкнуто относительно операции деления — при делении двух целых чисел не всегда получается целое число. Регулярные множества (и однозначно связанные с ними регулярные языки) замк­нуты относительно многих операций, которые применимы к цепочкам символов. Например, регулярные языки замкнуты относительно следующих операций:

· пересечения;

· объединения;

· дополнения;

· итерации;

· конкатенации;

· гомоморфизма (изменения имен символов и подстановки цепочек вместо символов).

Поскольку регулярные множества замкнуты относительно операций пересечения, объединения и дополнения, то они представляют булеву алгебру множеств. Суще­ствуют и другие операции, относительно которых замкнуты регулярные множе­ства. Вообще говоря, таких операций достаточно много.

Проблемы, разрешимые для регулярных языков

Регулярные языки представляют собой очень удобный тип языков. Для них раз­решимы многие проблемы, неразрешимые для других типов языков. Например, доказано, что разрешимыми являются следующие проблемы:

· Проблема эквивалентности. Даны два регулярных языка L1(V) и L2(V). Необходимо проверить, являются ли эти два языка эквивалентными.

· Проблема принадлежности цепочки языку. Дан регулярный язык L(V) и це­почка символов 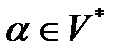. Необходимо проверить, принадлежит ли цепочка дан­ному языку.

· Проблема пустоты языка. Дан регулярный язык L(V). Необходимо прове­рить, является ли этот язык пустым, то есть найти хотя бы одну цепочку 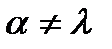, такую что .

Эти проблемы разрешимы вне зависимости от того, каким из трех способов за­дан регулярный язык. Следовательно, эти проблемы разрешимы для всех спосо­бов представления регулярных языков: регулярных множеств, регулярных грамматик и конечных автоматов. На самом деле достаточно доказать разрешимость любой из этих проблем хотя бы для одного из способов представления языка, то­гда для остальных способов можно воспользоваться алгоритмами преобразова­ния, рассмотренными выше.

Для регулярных грамматик также разрешима проблема однозначности — доказано, что для любой регулярной грамматики можно построить эквивалентную ей однозначную регулярную грамматику.

Три способа задания регулярных языков

Регулярные (праволинейные и леволинейные) грамматики, конечные автоматы (КА) и регулярные множества (равно как и обозначающие их регулярные выра­жения) — это три различных способа, с помощью которых можно задавать регулярные языки.