
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип математической индукции.
Для перехода от частных результатов, справедливых для отдельных значений n, к общим, верным при всех n, пользуются принципом математической индукции. Имеется некоторое утверждение А, зависящее определенным образом от натурального аргумента n, который принимает все целые положительные значения, начиная от р. Чтобы доказать справедливость утверждения А, поступают следующим образом:
1. убеждаются в справедливости А при n=р;
2. предполагают, что А верно при всех n, для которых p< n≤ k;
3. используя п.1 и 2, доказывают, что утверждение А справедливо при n=k+1.
Выполнение требований 1 – 3 позволяет от значения n=p, которое берется минимальным из всех возможных, шаг за шагом переходить к значениям р+1, р+2 и т.д. Поэтому считают, что выполнение требований 1 – 3 влечет за собой справедливость утверждения А для всех n > р. Это одна из аксиом натуральных чисел. Она называется аксиомой индукции.
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n ≥ p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом:
Если предложение А(n) истинно при n=p и если А(k)→ А(k+1) для любого k ≥ p, то предложение А(n) истинно для любого n ≥ p.
4. Собственный интеграл.
Определенный интеграл 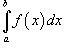 называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
· Предел a или b (или оба предела) являются бесконечными;
· Функция f (x) имеет одну или несколько точек разрыва внутри интервала [a,b].
Бесконечные пределы интегрирования
Пусть f (x) является непрерывной функцией в интервале [a, ∞). Несобственный интеграл определяется через предел следующим образом: называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
· Предел a или b (или оба предела) являются бесконечными;
· Функция f (x) имеет одну или несколько точек разрыва внутри интервала [a,b].
Бесконечные пределы интегрирования
Пусть f (x) является непрерывной функцией в интервале [a, ∞). Несобственный интеграл определяется через предел следующим образом:
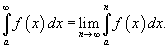 Рассмотрим также случай, когда функция f (x) непрерывна в интервале (−∞, b]. В этом случае несобственный интеграл определяется как
Рассмотрим также случай, когда функция f (x) непрерывна в интервале (−∞, b]. В этом случае несобственный интеграл определяется как
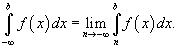 Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся. В противном случае интегралы расходятся. Пусть f (x) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение
Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся. В противном случае интегралы расходятся. Пусть f (x) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение
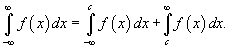 Если для некоторого действительного числа c оба интеграла в правой части сходятся, то говорят, что интеграл
Если для некоторого действительного числа c оба интеграла в правой части сходятся, то говорят, что интеграл  также сходится; в противном случае он расходится.
Теоремы сравнения
Пусть f (x) и g (x) является непрерывными функциями в интервале [a, ∞). Предположим, что также сходится; в противном случае он расходится.
Теоремы сравнения
Пусть f (x) и g (x) является непрерывными функциями в интервале [a, ∞). Предположим, что 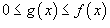 для всех x в интервале [a, ∞).
1. Если для всех x в интервале [a, ∞).
1. Если 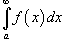 сходится, то сходится, то  также сходится;
2. Если также сходится;
2. Если  расходится, то расходится, то 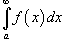 также расходится;
3. Если также расходится;
3. Если 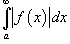 сходится, то сходится, то 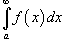 также сходится. В этом случае говорят, что интеграл также сходится. В этом случае говорят, что интеграл 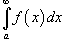 является абсолютно сходящимся.
Интеграл от разрывной функции
Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случаенесобственный интеграл определяется в виде является абсолютно сходящимся.
Интеграл от разрывной функции
Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случаенесобственный интеграл определяется в виде
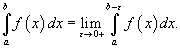 Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда
Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда
 Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися. Пусть f (x) непрерывна для всех действительных x в интервале [a,b], за исключением некоторой точки
Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися. Пусть f (x) непрерывна для всех действительных x в интервале [a,b], за исключением некоторой точки 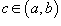 . Тогда справедливо соотношение . Тогда справедливо соотношение
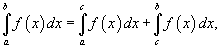 и говорят, что несобственный интеграл
и говорят, что несобственный интеграл 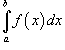 сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится. сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится.
|
| Пример |
Определить, при каких значениях k интеграл 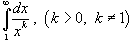 сходится.
Решение.
Используя определение несобственного интеграла, можно записать сходится.
Решение.
Используя определение несобственного интеграла, можно записать
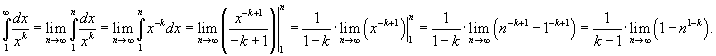 Из этого выражения видно, что существует 2 случая:
· Если 0 < k < 1, то
Из этого выражения видно, что существует 2 случая:
· Если 0 < k < 1, то 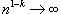 при при 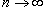 и интеграл расходится;
· Если k > 1, то и интеграл расходится;
· Если k > 1, то 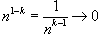 при при 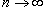 и интеграл сходится. и интеграл сходится.
|
Дата добавления: 2015-04-18; просмотров: 82; Мы поможем в написании вашей работы!; Нарушение авторских прав |